Con INESA TECH aprenderás cómo aplicar los aspectos fundamentales del análisis modal espectral. Si te interesa potenciar tus conocimientos, continúa leyendo la información que te presentamos en este artículo.
Base Teórica del Análisis Modal Espectral
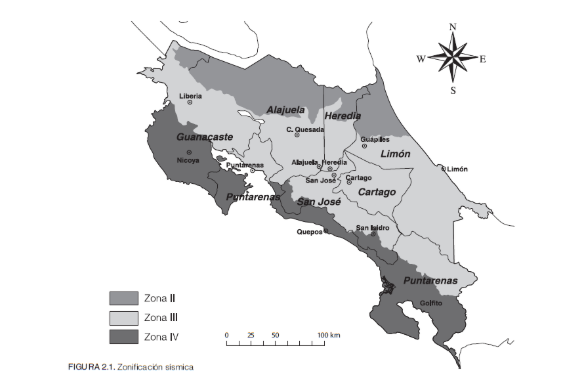
El análisis modal espectral a diferencia del método de fuerzas equivalentes considera la contribución de la masa de la estructura y la interacción de todos los modos de vibrar para la determinación del cortante basal y posteriormente los resultados de desplazamientos y fuerzas internas en cada uno de los elementos. Este análisis también toma en cuenta los espectros de diseño de cada región sísmica, es decir, se considera la aceleración del suelo y el período asociado a cada uno de los valores de aceleración del terreno. El análisis modal espectral toma como base la ecuación de equilibrio dinámico [1] para sistemas de un grado de libertad, la cual se muestra a continuación:
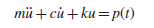
Donde m, c y k corresponde a las matrices de masa, amortiguamiento y rigidez del sistema respectivamente, mientras que el vector p(t) es el vector de la fuerza efectiva o equivalente del terreno.
Conceptos fundamentales
En el Análisis Modal Espectral, mediante la formulación de estas matrices, el cálculo del determinante de la matriz de rigidez y un factor λ multiplicado por la matriz de masa, se obtienen los llamados autovalores utilizando la función eigenvalores. Este concepto se explicará a continuación:
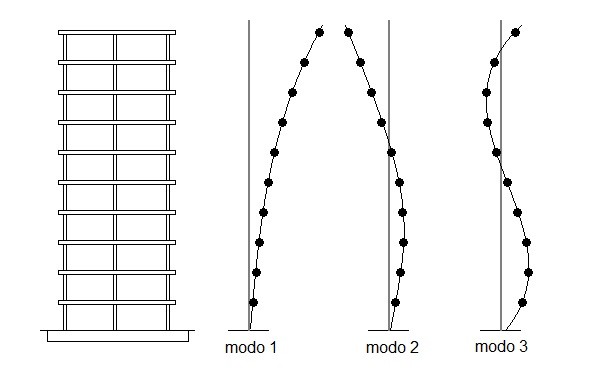
En álgebra lineal los eigenvalores y eigenvectores tienen diferentes aplicaciones en matemática e ingeniería. El concepto de eigenvalores se refiere a valores propios, al igual que los eigenvectores o vectores propios. Este concepto matemático en el análisis modal espectral proporciona información acerca del sistema dado que, los valores propios indican la frecuencia y el amortiguamiento de cada modo, y los vectores propios asociados a estos valores son vectores no nulos que indican la forma y dirección de cada uno de cada modo de vibración. Es decir, este vector permite definir el desplazamiento relativo de cada nivel de la estructura.
Una vez obtenida esta información se procede a revisar la ortogonalidad de los modos; este concepto hace referencia a que tan acoplados están los modos de vibrar del sistema; una estructura con acoplamiento en sus modos tendrá movimientos en varias direcciones simultáneamente en el mismo modo de vibración lo que ocasiona mayores esfuerzos en la los elementos.
Dado que en el análisis modal espectral el objetivo es determinar las frecuencias y modos de vibrar de la estructura, es imperativo conocer cuál es la contribución de cada modo de vibrar en la respuesta de la estructura; esto se traduce en una medida de que tanto contribuye el modo n en el sistema cuando este es sometido a fuerzas y desplazamientos. Cabe mencionar que esto está íntimamente relacionado con el valor de la masa y la rigidez de cada uno de los elementos estructurales.
Con el factor de participación sísmica, se determina la masa participativa modal o bien la masa modal efectiva βn de cada modo de vibrar, la sumatoria de estos valores debe ser mayor o igual al 90% de la masa total, esto para que los resultados sean representativos del sistema. Este porcentaje en el análisis modal espectral es importante debido a que con este análisis se obtendrán las fuerzas y desplazamientos en cada uno de los elementos estructurales, por lo que un porcentaje mucho menor a 90% da como resultado menores solicitaciones en el sistema que no corresponden a la respuesta real.
Si te ha interesado la información anterior, puedes profundizar estos conceptos en la Especialización en Ingeniería Estructural y Sismorresistente que brinda INESA TECH y dominar el análisis sísmico de estructuras.
Cálculo de la respuesta modal
Continuando con el análisis modal espectral, utilizando el espectro de respuesta de la zona sísmica de referencia, se realiza el cálculo de la respuesta modal para cada uno de los modos de vibrar. Para el caso del primer modo se utiliza la pseudoaceleración correspondiente al primer período o período fundamental de la estructura, con este valor se calcula la aceleración espectral y el desplazamiento relativo del primer modo.
Adicional a esto, se calcula el vector desplazamiento, el vector fuerza y el cortante en la base del modo 1. Este procedimiento se repite para cada uno de los modos teniendo en cuenta el valor de la seudoaceleración del espectro de respuesta y el período asociado a cada modo de la estructura. A continuación, se muestra una función de espectro de respuesta típica.
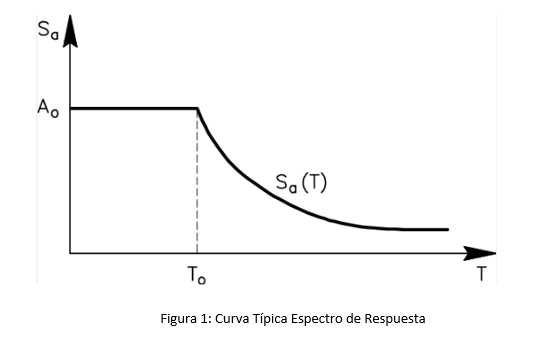
Combinaciones modales
Con el objetivo de definir la respuesta máxima de la estructura, el análisis modal espectral estipula que se debe realizar una combinación modal que se puede determinar por varios métodos, los 2 más utilizados corresponden al método SRSS o suma de los cuadrados y el método CQC que considera un coeficiente de correlación modal. La función principal de estos métodos es determinar de forma correcta los desplazamientos, fuerzas y cortantes máximos probables de cada nivel de la estructura que se utilizan para calcular las derivas. A continuación, se muestra la ecuación que caracteriza cada uno de los métodos de combinación modal.

Adicional a esto, se debe determinar la acción simultánea de las 2 componentes sísmicas horizontales mediante una combinación direccional que se puede dar de 2 maneras.
Combinaciones direccionales
SRSS:
Con esta combinación se determina la raíz cuadrada de la suma de los cuadrados de las solicitaciones en cada dirección, como se muestra a continuación:
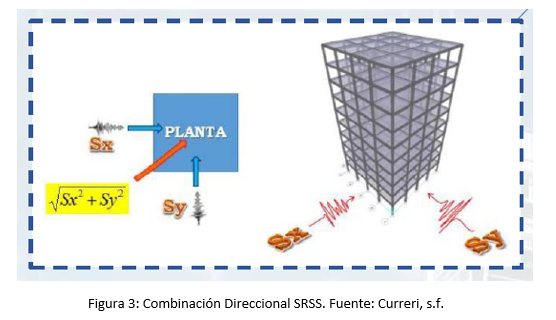
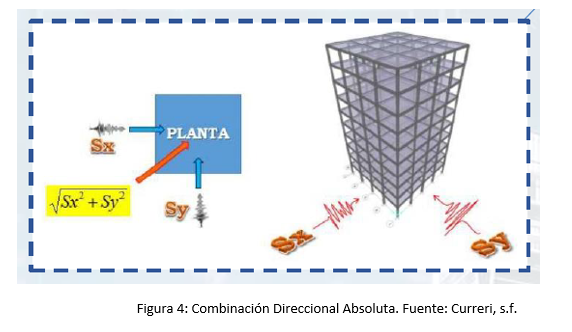
Absolute:
Con este método se determina el valor absoluto de las solicitaciones en una dirección más el 30% del valor absoluto de las solicitaciones en la dirección ortogonal. De igual forma este procedimiento se debe realizar a la inversa para obtener las fuerzas en ambas direcciones.
Referencias
- Chopra. (2017). Dynamics of Structures. Theory and Applications to Earthquake Engineering. University of Berkeley. 5° Edition.
- Instituto Científico Del Pacífico (s.f). Combinaciones Modales. [PDF]