Los métodos de análisis de puentes ante cargas de servicio se basan en tres aspectos fundamentales: equilibrio, compatibilidad de deformaciones y modelos constitutivos de naturaleza elástica lineal. Cualquier método empleado debe representar la rigidez relativa entre el tablero de concreto y las vigas. Los métodos de análisis dependen de la dimensionalidad espacial ya que los puentes pueden modelarse como sistemas en 1, 2, 2.5 y 3 dimensiones.
SISTEMA 1-D (MODELO DE VIGA)
Este modelo es atractivo para el diseño convencional y su respuesta obedece a la formulación de viga Euler-Bernoulli. La distribución de cargas vehiculares se realiza mediante el uso de factores de distribución, los cuales permiten representar el comportamiento de un sistema 3D mediante un modelo simplificado unidimensional.
De acuerdo con la especificación AASHTO LRFD 2017 se puede aplicar la metodología de los factores de distribución para puentes regulares; sin embargo, la misma se limita a sistemas que poseen sección transversal constante, vigas paralelas con similar rigidez y curvatura en planta despreciable. Las ecuaciones de factores de distribución mostradas en la norma se determinaron en base a cientos de análisis en puentes de distintos tipos, configuración geométrica y rigidez. Varios de estos puentes fueron analizados en programas computacionales y comparados con resultados experimentales. Las fórmulas propuestas por la AASHTO finalmente se basaron en los resultados de los programas que produjeron los resultados más aproximados.

Figura 1. Puentes Levadizos en la ciudad de Chicago. Fuente: Elaboración Propia.
SISTEMA 2-D (MODELO DE PARRILLA)
Los factores de distribución son de naturaleza aproximada y en caso de requerir un análisis más riguroso, se puede emplear el método de la parrilla, el cual representa un elemento continuo mediante elementos tipo barra, que poseen rigidez torsional y flexionante. Este método se volvió popular en los años 60 con el advenimiento de las computadoras digitales y la facilidad de programación con los métodos de análisis matricial. Una de las ventajas del sistema 2D es que los resultados obtenidos mediante un software de análisis pueden interpretarse fácilmente mediante diagramas de cuerpo libre y equilibrio global.
Propiedades geométricas de los elementos
Las propiedades torsionales y de flexión de los elementos longitudinales y transversales se basan en las secciones no agrietadas, usando el concepto de ancho tributario. Para un tablero de concreto apoyado sobre vigas metálicas, el momento de inercia (Ig) de un elemento compuesto se calcula mediante:

Mientras que la constante torsionante de la sección compuesta se obtiene a partir de:


Debe asignarse cada propiedad de inercia y torsión a cada elemento que conformará el sistema de análisis tipo parrilla.
Configuración del Modelo en Software de Análisis Estructural
Una vez calculadas las propiedades de flexión y torsión, puede usarse un software tal como SAP2000 para efectuar el análisis estructural para la posición crítica de los vehículos HL93 (camión de diseño) que produzcan el momento máximo positivo, el cual usualmente ocurre al 40% de la luz del primer tramo exterior en un puente continuo. Se ha realizado la modelación de un puente de dos tramos con longitud de vano igual a 15 metros y tablero de concreto soportado monolíticamente por vigas metálicas.
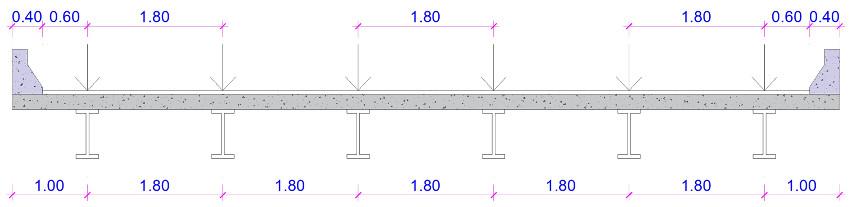
Figura 2. Sección transversal de puente y ubicación de camiones de diseño HL93. Fuente: Elaboración Propia.
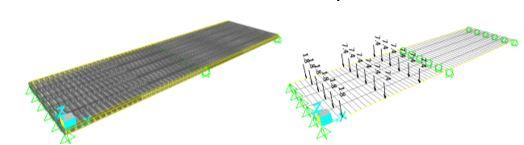
Figura 3. Modelo tridimensional de puente – Grillage Method SAP2000. Fuente: Elaboración Propia.
A continuación, se muestra el resultado del máximo momento flector obtenido en una viga interior
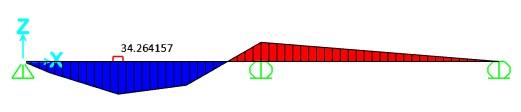
Figura 4. Momento máximo positivo en viga interior de puente – Grillage Method SAP2000. Fuente: Elaboración Propia.
MOMENTO MÁXIMO OBTENIDO MEDIANTE LOS FACTORES DE DISTRIBUCIÓN Y VALIDACIÓN DEL MÉTODO DE LA PARRILLA
Para el puente continuo de dos tramos mostrado, se realizó el análisis de viga unidimensional en el software FTOOL empleando un análisis del tipo “moving load”, obteniendo la siguiente envolvente de momentos flexionantes
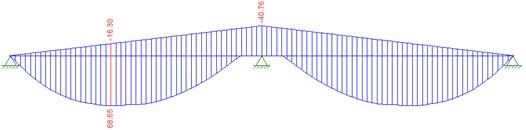
Figura 5. Momento máximo positivo en viga unidimensional – FTOOL. Fuente: Elaboración Propia.
El factor de distribución gMI_M se calcula según la especificación AASHTO LRFD 2017 – Tabla 4.6.2.2.2b-1, para el caso de múltiples carriles cargados

Reemplazando estos parámetros se obtiene un valor de gMI_M = 0.52, por lo tanto, el momento máximo obtenido aplicando los factores de distribución es:

De acuerdo con estos resultados, se puede observar que el momento máximo calculado mediante un método simplificado (factores de distribución) es muy cercano al obtenido con un modelo refinado como lo es el método de la grilla (grillage method) y ambos pueden usarse en el análisis de puentes convencionales.