La resistencia de materiales es una disciplina fundamental en la ingeniería estructural que estudia el comportamiento de los materiales bajo la acción de cargas externas. Comprender los principios básicos permite diseñar estructuras seguras y eficientes, optimizando su desempeño ante distintas solicitaciones. Este artículo aborda los conceptos esenciales de tensiones, deformaciones, comportamiento de materiales y otros aspectos clave para la ingeniería estructural y sismorresistente.
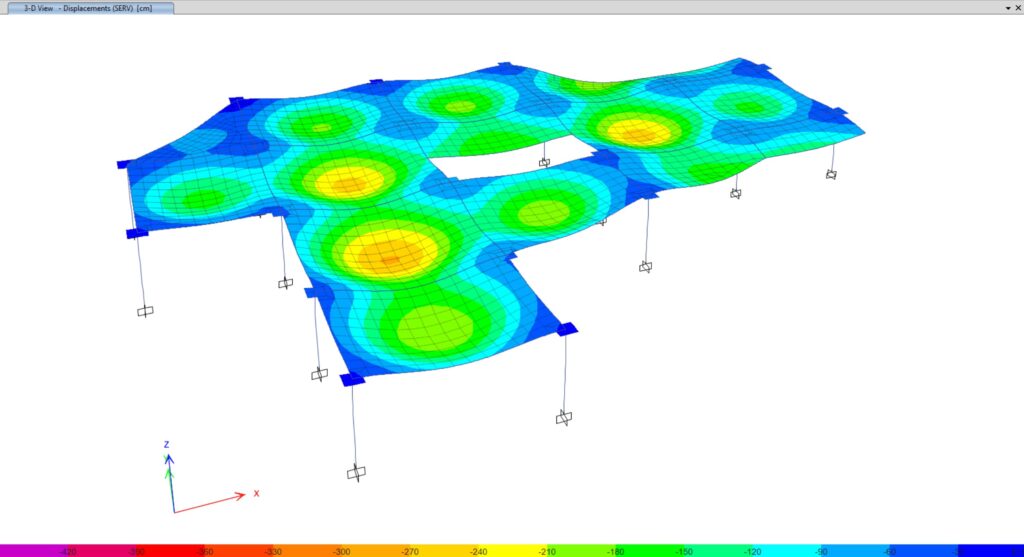
Figura N°1 – Deformada de una losa maciza ante cargas gravitacionales en ETABS
Esfuerzos y Deformaciones
Cuando un material es sometido a una carga externa, experimenta fuerzas internas conocidas como tensiones. Estas tensiones se clasifican en:
Esfuerzo Normal (σ): Se produce cuando una fuerza actúa perpendicular a la sección transversal del material. Se expresa como:
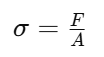
Donde:
– F es la fuerza aplicada
– A es el área de la sección transversal.
Esfuerzo Cortante (τ): Ocurre cuando una carga actúa paralelamente a la sección transversal, generando deslizamiento interno entre capas del material:
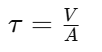
Donde:
– V es la fuerza cortante
– A es el área de la sección transversal.
Deformación Longitudinal (ε): Es la variación de longitud respecto a la original:
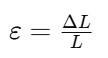
Donde:
– ΔL es el cambio de longitud
– L es a longitud inicial.
Deformación Cortante (γ): Relacionada con la distorsión angular en un material bajo esfuerzos cortantes.
En la mayoría de los casos, el análisis estructural requiere evaluar las tensiones y deformaciones en función del estado de cargas, considerando efectos adicionales como temperatura y fluencia en materiales viscoelásticos.
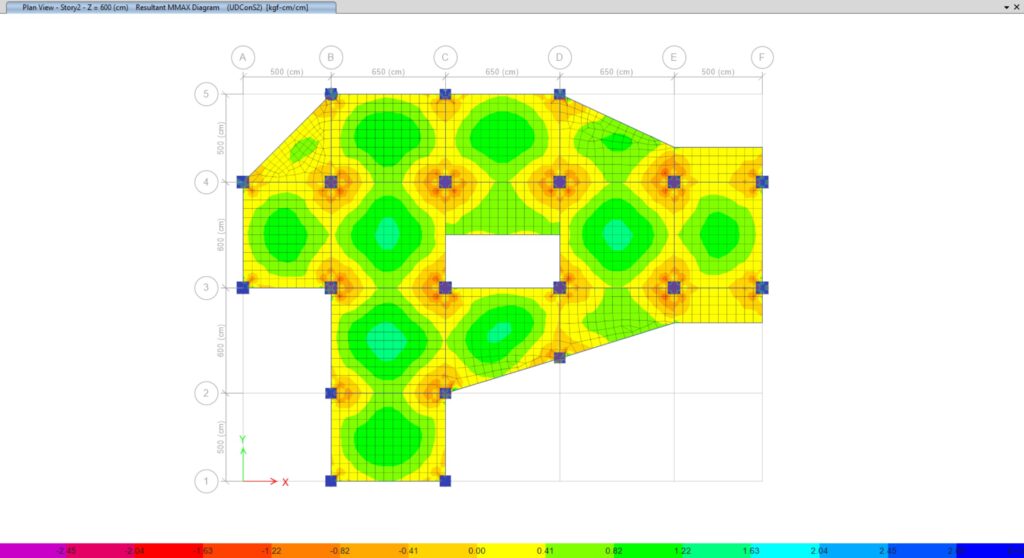
Figura N°2 – Momentos máximos en una losa maciza ante cargas gravitacionales en ETABS
Módulo de Elasticidad y Ley de Hooke
El módulo de elasticidad (E) o módulo de Young mide la rigidez de un material, es decir, su resistencia a la deformación elástica bajo carga. Se expresa como:
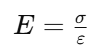
Este concepto es crucial en el análisis de estructuras, ya que permite predecir su comportamiento bajo cargas normales. Los materiales con un módulo de elasticidad alto, como el acero, presentan menor deformación ante cargas aplicadas en comparación con materiales más flexibles como la madera o el hormigón sin refuerzo.
Adicionalmente, el módulo de elasticidad varía con la temperatura y las condiciones ambientales, lo que influye en el comportamiento estructural a largo plazo.
Fatiga y Comportamiento Bajo Cargas Cíclicas
Las estructuras no solo soportan cargas estáticas, sino también cargas variables en el tiempo. La fatiga de materiales se refiere a la degradación progresiva del material cuando es sometido a cargas repetitivas. Este fenómeno puede ocasionar fallas inesperadas incluso si las tensiones aplicadas son menores a la resistencia última del material.
Los ingenieros estructurales evalúan la fatiga mediante:
- Curvas de Wohler (S-N): Relacionan el número de ciclos con la tensión aplicada hasta la falla.
- Criterios de diseño para vida infinita: Se diseñan estructuras para operar bajo un límite de tensión seguro.
- Mecanismos de propagación de grietas: Se emplean modelos de fractomecánica para predecir la propagación de defectos en materiales sometidos a carga cíclica.
Si te ha interesado la información anterior, puedes profundizar estos conceptos en la Especialización en Ingeniería Estructural y Sismorresistente que brinda INESA TECH y dominar el análisis sísmico de estructuras.
Teoría de Esfuerzos y Estados de Carga
En la práctica, los materiales están sometidos a múltiples combinaciones de esfuerzos, lo que requiere el uso de criterios de falla:
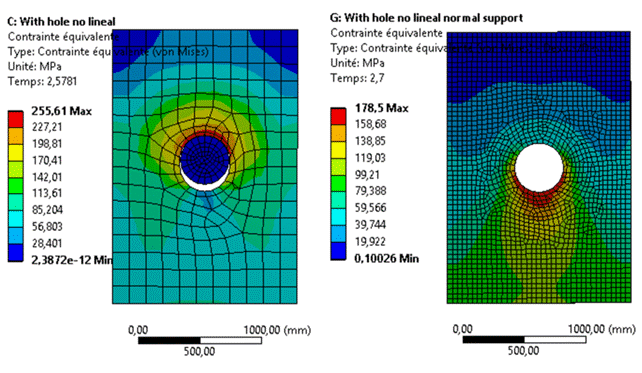
- Teoría de Von Mises: Aplicada a materiales dúctiles, establece que la falla ocurre cuando la energía de distorsión alcanza un valor crítico.
- Teoría de Mohr-Coulomb: Utilizada en materiales frágiles como concreto, combina esfuerzos normales y cortantes para predecir la falla.
- Resistencia Última y Factor de Seguridad: Se emplean coeficientes de seguridad para garantizar márgenes adecuados de resistencia estructural, ajustando los valores de diseño en función de incertidumbres en cargas y materiales.
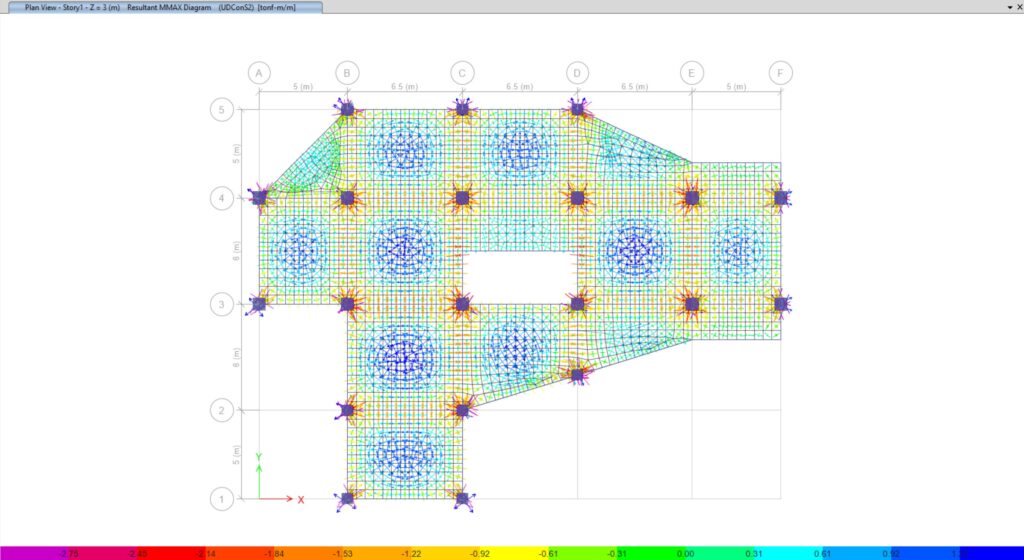
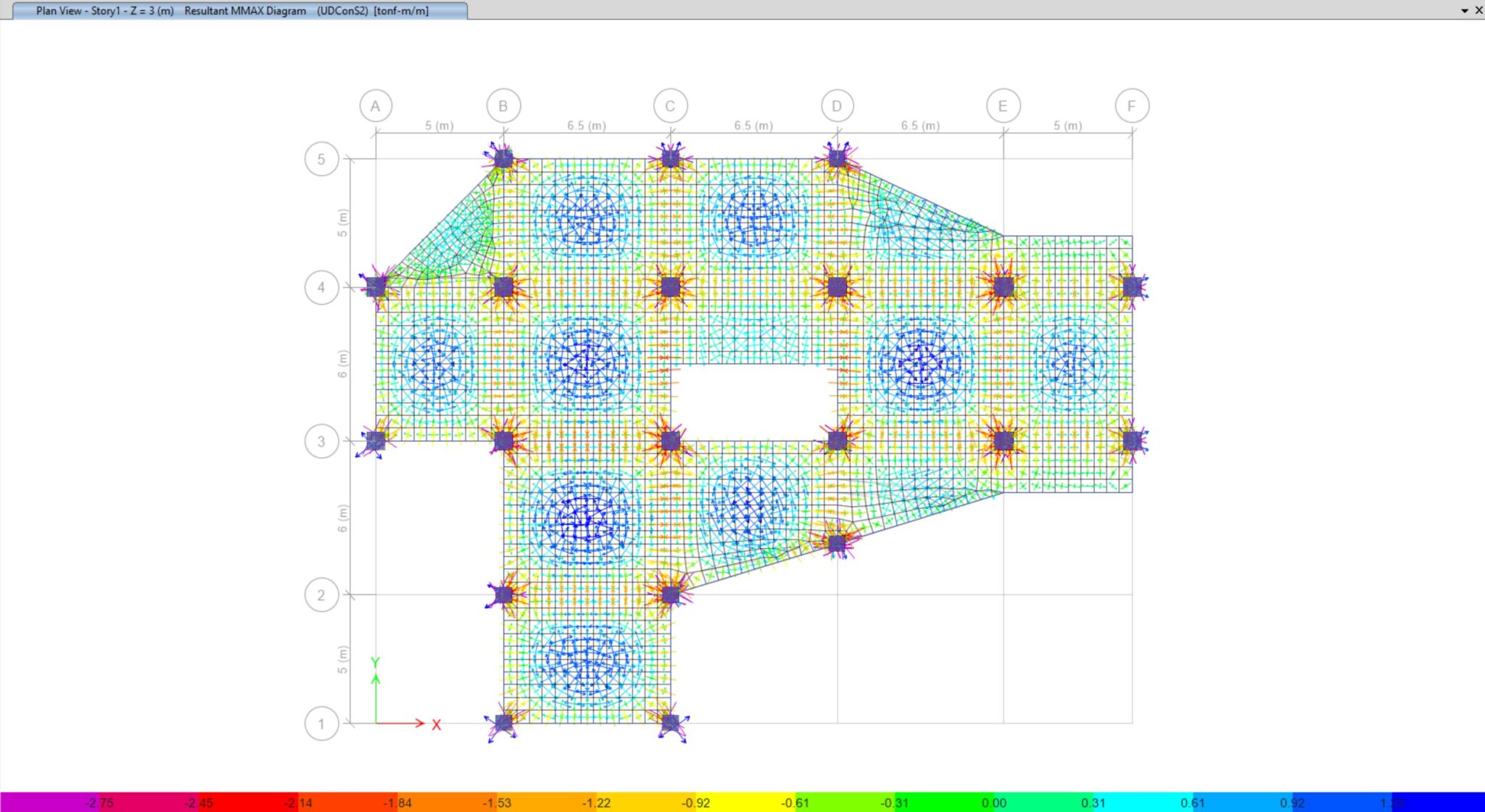
Figura N°3 – Resultantes de momentos máximos con flechas en una losa maciza ante cargas gravitacionales en ETABS, conforme al Círculo de Mohr
Análisis de Pandeo y Estabilidad
Las estructuras delgadas y esbeltas, como columnas y vigas, pueden fallar por pandeo antes de alcanzar su resistencia última. La carga crítica de pandeo de una columna se estima mediante la ecuación de Euler:
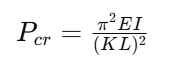
Donde:
– P_cr es la carga crítica,
– I es el momento de inercia,
– k es el coeficiente de longitud efectiva,
– L es la longitud no soportada de la columna.
El pandeo es un factor crítico en el diseño de estructuras sometidas a compresión, como pilares y elementos de puentes. En estructuras sometidas a cargas dinámicas, se debe considerar el pandeo inducido por vibraciones y efectos de segundo orden.
Consideraciones en Ingeniería Sismorresistente
Las estructuras en zonas sísmicas están sujetas a cargas dinámicas complejas, lo que exige un diseño basado en principios de ductilidad, disipación de energía y amortiguamiento. Entre los aspectos clave se incluyen:
- Capacidad de disipación de energía mediante diseño plástico controlado.
- Uso de materiales con adecuada capacidad de deformación antes de la falla
- Diseño de conexiones y uniones flexibles para absorber cargas sísmicas.
- Evaluación de comportamiento dinámico mediante análisis tiempo-historia y espectral..
- Utilización de dispositivos de disipación de energía y aislamiento sísmico para mejorar la respuesta estructural.
Mantente actualizado en el sector AEC con nuestros Cursos, Especializaciones y Másteres en el ámbito del BIM y las nuevas tecnologías aplicadas a la construcción:
Referencias
- Gere, J. M., & Goodno, B. J. (2012). Mechanics of Materials (8th ed.). Cengage Learning.
- Beer, F. P., Johnston, E. R., DeWolf, J. T., & Mazurek, D. F. (2014). Mechanics of Materials (7th ed.). McGraw-Hill.
- Timoshenko, S. P., & Gere, J. M. (1961). Theory of Elastic Stability (2nd ed.). McGraw-Hill.
- Chopra, A. K. (2017). Dynamics of Structures: Theory and Applications to Earthquake Engineering (5th ed.). Pearson.